The goal is to find an optimal combination of different components constituting a resilient system structure. The development of problem-specific models and mathematical optimization techniques for the solution of the resulting mixed-integer nonlinear optimization problems is essential.
System approach opens up greater optimization potential
In the second funding period of the CRC 805, the use of discrete optimization methods for system design was pursued within the approach TOR (Technical Operations Research). This approach will be continued in the new subproject A9 in the third funding period, and will be extended by the concept of resilience. By this, two aspects are addressed: On the one hand, a greater optimization potential can be used by a systemic view. On the other hand, taking into account the interaction of the system's components is possible. This allows to deal with uncertainty on a holistic level.
Optimization of technical systems
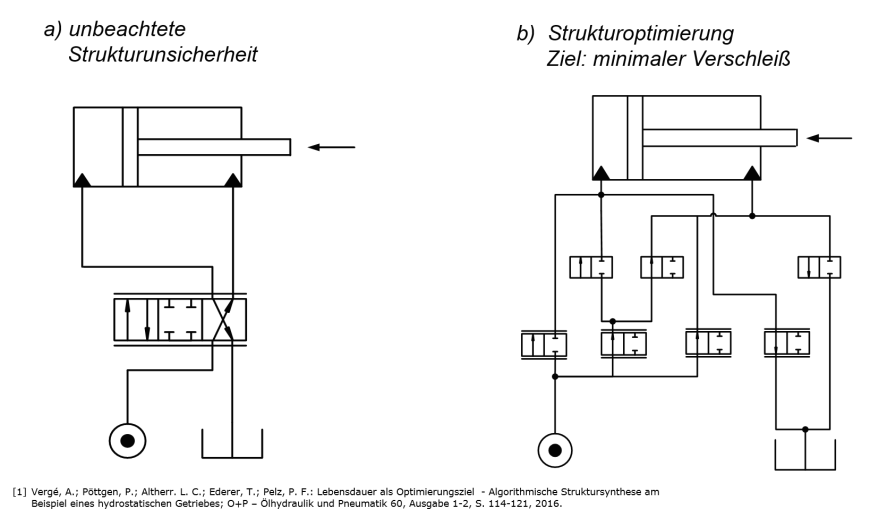
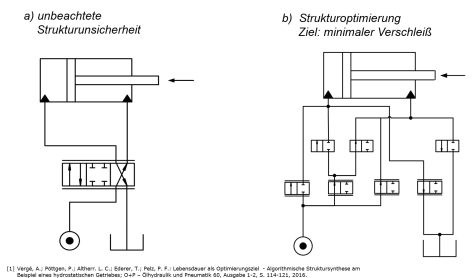
Thanks to interdisciplinary cooperation within CRC 805, the system structure and the operation of a wide range of technical systems have already been optimized: pumping, heating and ventilation systems have been optimally designed using mathematical optimization methods. An experimental validation for the example of a booster system showed that in the worst case the solutions found differ by 10% from the predicted optimum. An optimal system structure has also been found for the drive train of a hydrostatic transmission for the CRC demonstrator, c.f. the figure below.
Increasing resilience
In order to increase the resilience in the system design, target criteria and constraints are formulated and integrated into a mathematical optimization model. These are based on several resilience metrics: the level of system functionality after component failure, the functional range of the system and its k-reliability. If a system is k-reliable, k components can fail and it still fulfills a previously defined minimum function. If one takes the k-reliability of a technical system into account, the corresponding mathematical optimization model gets multi-stage, since an emergency function must be guaranteed for each combination of a previously specified maximum number k of failed components. As this greatly increases the complexity of the models, we plan to deal with it by treating individual scenarios in a first step. To keep the problem size as small as possible, we iteratively generate particularly critical scenarios in a second step, which are then treated explicitly.
Subproject Managers
| Photo | Name |
|---|---|
|
A
| Dr.-Ing. Lena Altherr |
|
P
| Prof. Dr. Marc Pfetsch |